Blog

Sorting Algorithms from Four Semesters of Computer Science in 5 Hours by Brian Holt
Posted on August 18, 2020 in Algorithms, JavaScript by Matt Jennings

See the trekhleb / javascript-algorithms GitHub repo for JavaScript algorithms (including sorting algorithms) showing complexity, including time and space complexity.

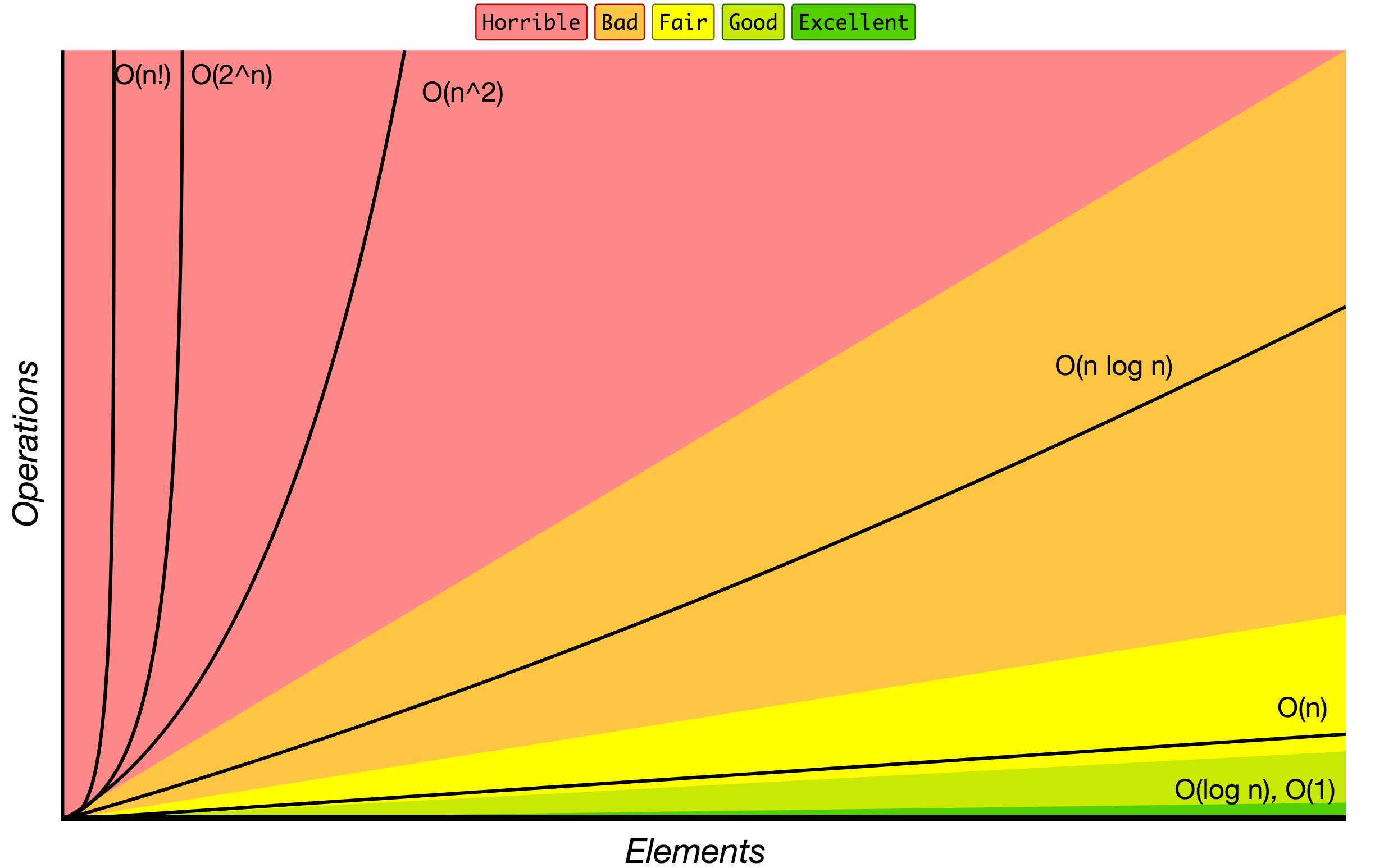
Here’s an image from that GitHub repo showing a graph of operations vs elements. O(1) is the fastest and O(n!) is the slowest.

Insertion Sort

According to the GitHub repo link above, and Four Semesters of Computer Science in 5 Hours by Brian Holt, Insertion Sort [algorithm complexity is n at best; n^2 at average and worst; and in memory is constant or 1] is faster than Bubble Sort but slower than other sort methods like Quick Sort [algorithm complexity is n log(n) at best and average; n^2 at worst; and log(n) in memory], NOT taking memory into account. It is a stable sorting algorithm which means that it maintains the order of the equal elements.

If you take memory into account and it’s limited, then Insertion Sort could be faster than other methods such as Quick Sort that use more memory.

Code example:

const insertionSort = nums => {
  /*
  Start iterating at an index of 1 because
  In the nested for loop below (with j as the index)
  then the number at index of j will
  have start sorted as it will be on the left side
  and be a single array element (have a length of 1)
  */
  for(let i = 1; i < nums.length; i++) {
    for(let j = 0; j < i; j++) {
      
      if(nums[i] < nums[j]) {
        /*
        The sliced variable below is assigned to the nums array
        which at index i removes 1 element 
        from the nums array and returns the existing array as
        it is a destructive method on the array
        */
        const spliced = nums.splice(i, 1);
        /*
        Modifies the array and
        at index j, 
        0 (2nd argument) means that no items will be removed
        and spliced[0] (3rd argument) means that after index j 
        the new array, or sliced[0] will be added
        */
        nums.splice(j, 0, spliced[0]);
        
      }
    }
  }
  
  return nums;
};


console.log(insertionSort([10,5,3,8,2,6,4,7,9,1]));
// Output:
// [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

Merge Sort

In JavaScript the .sort() array method is usually run as a Merge Sort by most browsers and the best, average, and worst algorithm complexity is n log(n). It is a stable sorting algorithm which means that it maintains the order of the equal elements.

Code example:

const mergeSort = nums => {
  if(nums.length < 2) return nums;
  
  const length = nums.length;
  const middle = Math.floor(length / 2);
  // .slice() array method creates a new array
  // and below starts at index 0 and goes to the index JUST BEFORE
  // index middle and .slice() is non-destructive
  const left = nums.slice(0, middle);
  // Goes from middle index to the very last index
  const right = nums.slice(middle);
  
  return stitch(mergeSort(left), mergeSort(right));
};

const stitch = (left, right) => {
  const results = [];
  
  // If the array is not empty because
  // an empty array would have a length of 0 which is falsy
  while(left.length && right.length) {
    if(left[0] <= right[0]) {
      // Push the first element (or left[0]) and push it into results
      results.push(left.shift());
    } else {
      results.push(right.shift());
    }
  }
  
  while(left.length) {
    results.push(left.shift());
  }
  
  while(right.length) {
    results.push(right.shift());
  }
  
  return results;
}

const nums = [10,5,3,8,2,6,4,7,9,1];

Quick Sort

Quick Sort is at best and average n log (n) but at worst n^2 (for example when you always choose the last index as the pivot and the list is already sorted). It takes less memory than Merge Sort but is also unstable.

Example code:

const quickSort = nums => {
  if(nums.length <= 1) return nums;
  
  const pivot = nums[nums.length - 1];
  const left = [];
  const right = [];
  
  for(let i = 0; i < nums.length - 1; i++) {
    if(nums[i] < pivot) {
      left.push(nums[i]);
    } else {
      right.push(nums[i])
    }
  }
  
  return [...quickSort(left), pivot, ...quickSort(right)];
  
}

console.log(quickSort([10, 8, 2, 1, 6, 3, 9, 4, 7, 5]));